Normal dağılım, istatistiksel analizlerde en sık karşılaşılan olasılık dağılımlarından biri olup birçok parametrik testin temel varsayımını oluşturur. Verilerin normal dağılıma uyup uymadığını belirlemek, doğru analiz yöntemlerini seçmek açısından kritik bir adımdır. Bu makalede, normal dağılımın tanımını, temel özelliklerini ve SPSS kullanarak normal dağılım analizinin nasıl yapılacağını adım adım inceleyeceğiz.
Normallik Testi Nedir?
Akademik çalışmalarda araştırmacıların verileri analiz aşamasına getirmeden önce en başta yapması gereken temel analizler bulunmaktadır. Bu analizlerin başında normallik analizi ya da normallik testi gelmektedir. Bu aşamada verilerin analizlerinde hangi metotları uygulayacağımıza karar veren önemli bir aşamadır. Bu sebeple dikkatli bir düzeyde çıkan sonuçları incelemek ve yorumlamak gerekmektedir. Yorumlama aşamasında belirleyeceğimiz kaynaklar da oldukça önemlidir. Bu sebeple karar verme aşamasında desteklemek amacıyla kaynak bulmanız ve tezlerinizde, akademik makalelerinizde bunu belirtmelisiniz. Ortaya çıkan sonuçlar neticesinde verilerin normal dağılım sergileyip sergilemediğini görebilirsiniz.
Verilerin genellikle normallik analizi ile normal dağılım sergilemesi yani parametrik olması beklenmektedir. Çünkü bu durum araştırmadan elde ettiğimiz sonuçların daha güvenilir olduğunu göstermektedir. Bu sebeple normal dağılım sergilenmeyen verilerde ise verilerin dönüştürülmesi metodu uygulanmaktadır. Bu kısmı sonra ele alacağız.
Normal Dağılım Testi Neden Yapılır?
Makalemizde bahsettiğimiz gibi verilerin parametrik değerlere sahip olması araştırma sonucunun güvenirliği açısından oldukça önemlidir. Bu sebeple normal dağılım testi yani normallik analizi aşamasını yapıp elde edilen sonuçlar ile parametrik testleri uygulamamız gerekmektedir. Parametrik testlerde aşağıda yer alan durumlar ile gerçekleştirebiliriz;
- Verilerin en az aralık ölçeğinde olması,
- Verilerin normal dağılım sergilemesi,
- Birden fazla grubun olması durumunda grupların varyanslarının eşit dağılması gerekmektedir.
Normallik analizi aşamasında öncelikle bilinmesi gereken husus örneklem sayısının 30’un altında olmaması gerekliliğidir. 30’un altında yer alan örneklem grubu normal dağılım sergilememektedir.
Hangi Normallik Testi Kullanılmalı
Normallik testinde öncelikle normal dağılım sergilemesi özelliklerine sahip olması gerekmektedir;
- Normal dağılım eğrisi çan eğrisine benzer olmaktadır ve normal dağılım hakkında temel düzeyde bir bilgi verecektir. Bu amaçla histogram, kutu çizgi grafiği, gövde ve yaprak diyagramı gibi grafikler kullanılabilmektedir. Makalemizde bunlara detaylı yer verilecektir.
- Normal dağılım sergilediğini gösteren bir diğer özellik ise mod, medyan ve ortalama değerlerinin birbiri ile eşit düzeyde olmasıdır. Bu değerlerin birbirlerine yakın olması da normal dağılım olarak kabul edilir.
- Momentlere dayanan eğiklik ve basıklık durumları da normal dağılımı gösteren bir diğer özelliktir. Bu durumda α3 eğiklik değerinin “0” değerinde olması ve basıklık ölçüsü olan α4 değerinin ise “3” olması dağılımın normal dağıldığını göstermektedir. Normal dağılım sergileyen verilerin nasıl raporlandığını görmek için tıklayınız. Normal dağılım sergilemeyen analiz örneği için tıklayınız.

Spss Normallik Testi
Spss programında normallik testlerini Kolmogorov-smirnov testi ve shapiro-wilk testi ile test etmekteyiz.
Kolmogorov-Smirnov Testi
Kolmogorov-smirnov testi elde olan verilerin evren üzerinde normal dağılıma sahip olduğunu göstermektedir. Spss’te Kolmogorov-smirnov testi aşamasında resimde görüldüğü gibi yapılması gerekmektedir.

Şekilde görüleceği üzere tests of normality tablosunda Kolmogorov-smirnov’un sig yani p değerinin ,105 olduğu yani p>,05’ten büyük olması nedeniyle verilerin normal dağılım sergilediği görülmektedir. Normallik testi p değeri bu aşamalarda bulunmaktadır.
Shapiro-Wilks Testi
Normal dağılım testlerinden bir diğeri ise Shapiro-Wilks testidir. Bu test veri evreninin normal dağılımı sergileyip sergilemediğini gösterir. Bu testte de sig. değeri 0,05’ten büyük olması durumunda verilerin normal dağılım sergilediği kabul edilmektedir. Gözlem sayısı 30’un üzerinde olması durumunda Kologorov-Smirnov, 30’un altında olması durumunda ise Shapiro-Wilks testine bakılmaktadır.
Normal Dağılım Tablosu
Normal dağılım tablosu akademik çalışmalarda çok fazla karşımıza çıkan bir işlem olmaktadır. Normallik testi spss programında yapabilmek için;
Analyze<Descriptive Statistic<Explore kısmına girildikten sonra normal dağılımı kontrol edeceğimiz veriyi dependent list kısmına aktarıyoruz. Plot kısmına tıklayarak Normality plots with test ve descripitive kısmından stem-and-leaf ve histogram kısmını işaretleyip continue kısmına tıklıyoruz. En son aşama olarak OK kısmına tıklayarak sonuçları elde ediyoruz. Normallik testi spss programında bu aşamalar ile yapılmaktadır.
Elde ettiğiniz sonuçları spss normallik testi yaparak yorumlayabilirsiniz. Ancak raporlama kısmı oldukça farklıdır. Normal dağılım tablosunda spss programından elde edilen çıktı üzerinden raporlama düzeni normal dağılım tablosu resminde görebilirsiniz. Tabloyu oluşturduğumuzda kologorov-Smirinov testinde normallik testi p değeri ,000 olduğu zaman basıklık ve çarpıklık değerleri incelenir. Bu değerlerin ±2 arasında olması gerekmektedir. Spss normallik testi yorumlama aşaması da bu şekilde olmaktadır. Bu tablo normallik analizi spss te elde edildikten sonra standart normal dağılım tablosu olarak raporlanmaktadır.
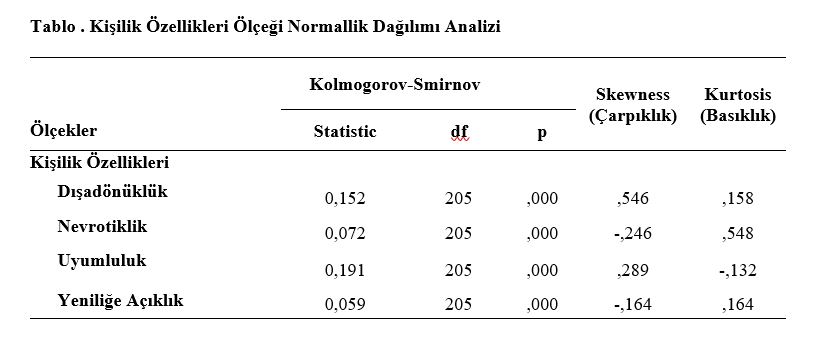
Normal Dağılım Grafiği
Normallik analizi tablolar ve grafikler yardımı ile yorumlanmaktadır. Grafikler bizlere verilerin uç değerlerini, saçılımlarını ve beklenen ile elde edilen sonuçlar arasında ki farkları göstermektedir.
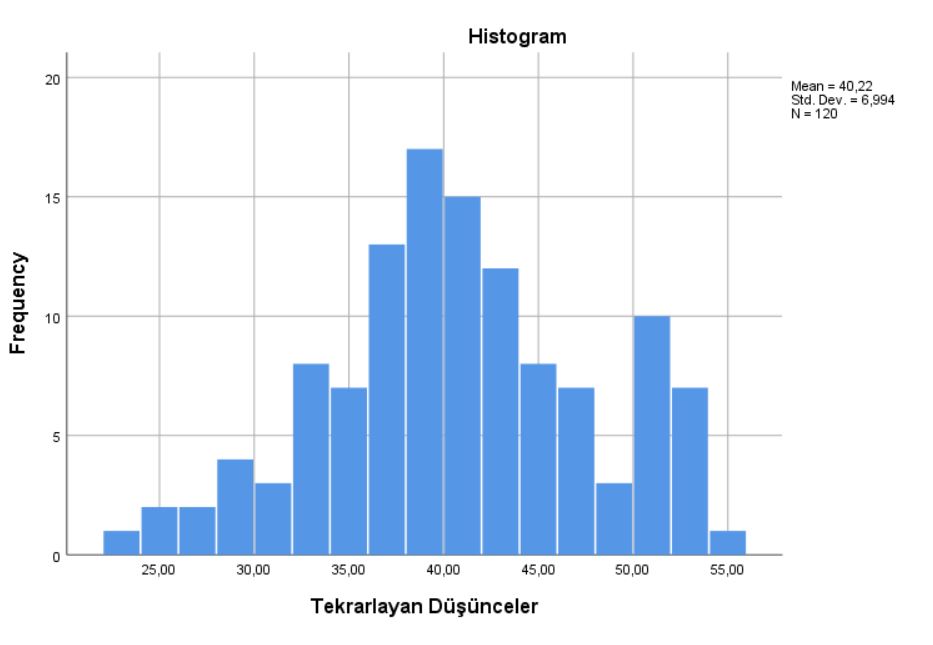
Histogram Grafiği
Histogram grafiğinde normallik analizi aşamasında eğer ki veriler normal dağılım sergiliyor ise simetrik bir çan eğrisi düzeyinde gözükmektedir. Ancak histogram grafiği normallik analizi için tek başına yeterli bir bulgu olmamaktadır.
Normal Q-Q Plot Grafiği ve Eğiliminden Arındırılmış Q-Q Grafiği
Normal Q-Q Plot grafiği, bu grafikte beklenen ile gözlenen değerler arasında oluşan ilişkiyi göstermektedir. Dağılımın normal olduğunu anlayabilmek için 45 derecelik bir açı sağlayan doğru ortaya çıkar.
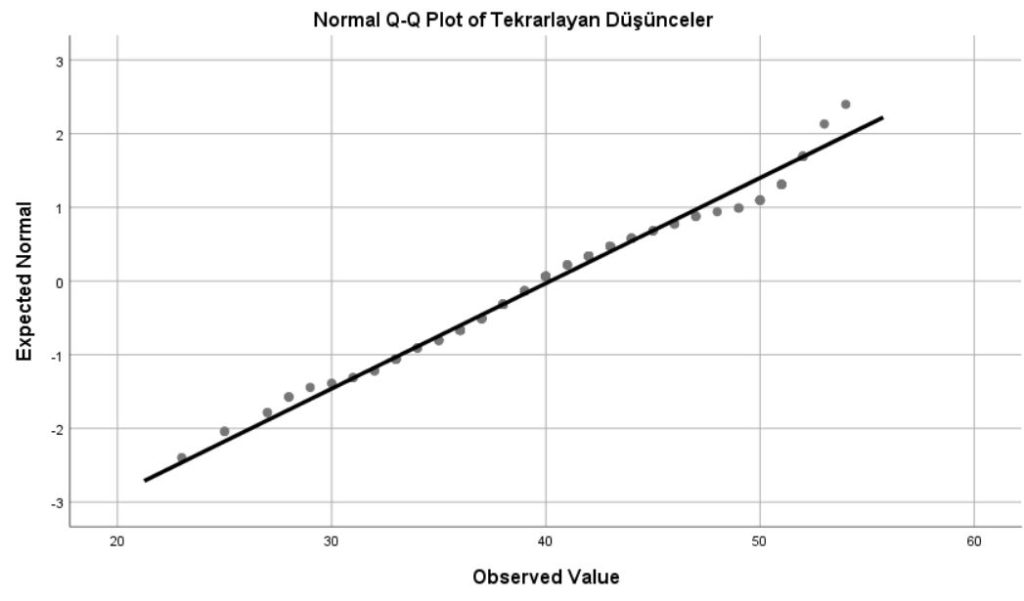
Eğiliminden arındırılmış Q-Q grafiğinde ise normallik analizi aşamasında normal dağılım gösteriyorsa yatay sıfır çizgisi yakınında ve belli bir şekli olmayan dağılım halinde kendisini gösterir.
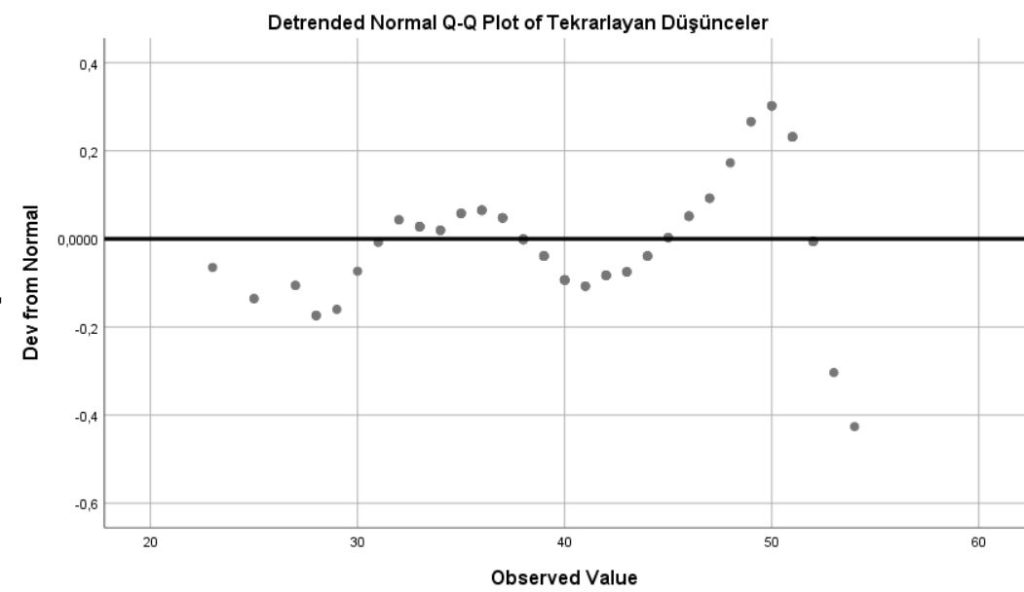
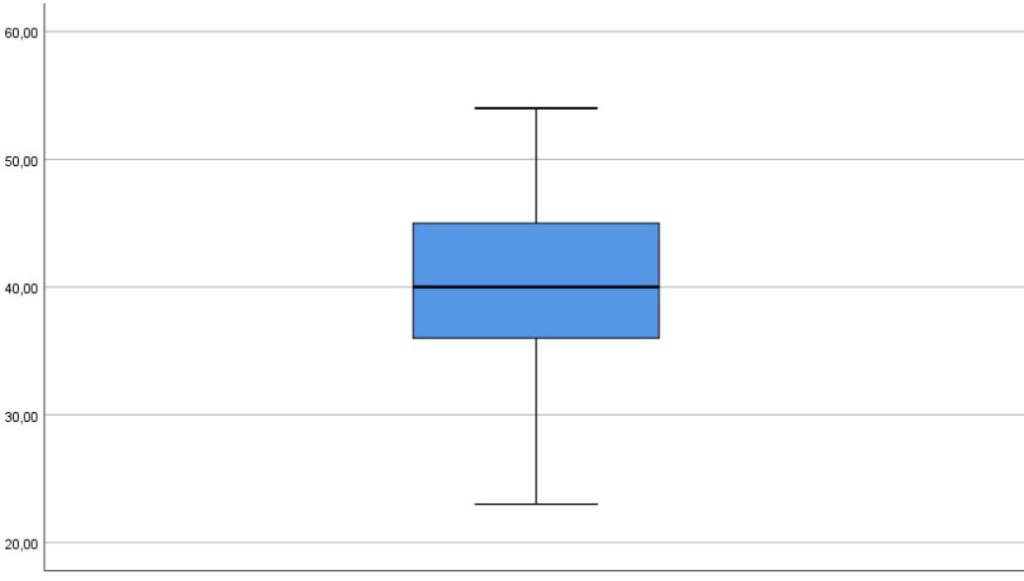
Kutu Çizgi Grafiği
Bu grafikte normal dağılımı görebilmek için üst ve alt kısımda kalan dikey çizgilerin boylarının birbirine neredeyse yakın ve kutunun yatay çizgisinin ortalaması beklenmektedir (Can, 2019).
Burada yer alan grafikler üzerinden sadece normallik analizi yaparak yorumlamak doğru olmamaktadır. Bu sebeple yukarıda bahsettiğimiz normallik analizi aşamalarını dahil etmelisiniz. Bu normal dağılım grafiği ile uç değerleri de görebilir ve verileriniz ile ayıklama işlemi yapabilirsiniz.